Datenklassifizierung mit neuronalen Netzen
Ein eindeutiger Kompromiss zwischen parametrischen und metrischen Methoden ist die Verwendung von neuronalen Netzen zur Lösung von Klassifizierungsproblemen. Neuronale Netze sind nichtparametrische Modelle, die keine Annahmen über die Wahrscheinlichkeitsverteilung der Daten erfordern, aber auch keine Abstandsmaße verwenden. Dies macht sie zu universellen Klassifikatoren, die auch in Fällen Ergebnisse liefern, in denen parametrische und metrische Klassifikatoren keine akzeptable Lösung bieten.
Die Klassifizierung ist eine der wichtigsten Aufgaben des Data Mining. Sie wird mit Hilfe analytischer Modelle, so genannter Klassifikatoren, gelöst. Die Nachfrage nach der Klassifizierung ist auf die relativ einfache Anwendung von Algorithmen und Methoden sowie auf die hohe Interpretierbarkeit der Ergebnisse im Vergleich zu anderen Datenanalysetechniken zurückzuführen.
Gegenwärtig wurde eine große Anzahl verschiedener Arten von Klassifikatoren entwickelt, für deren Konstruktion sowohl statistische Methoden (logistische Regression, Diskriminanzanalyse) als auch Methoden des maschinellen Lernens (neuronale Netze, Entscheidungsbäume, k-nearest neighbours-Methode, Support Vector Machines usw.) verwendet werden.
Die Notwendigkeit, bei der Datenanalyse eine große Anzahl verschiedener Klassifizierungsmethoden einzusetzen, ergibt sich aus der Tatsache, dass die Probleme, die mit ihrer Hilfe gelöst werden sollen, ihre eigenen spezifischen Merkmale haben können, die beispielsweise mit der Anzahl der Klassen (binäre Klassifizierung oder mit mehreren Klassen) oder mit der Darstellung der Originaldaten - ihrem Umfang, ihrer Dimensionalität und ihrer Qualität - zusammenhängen, was die Auswahl eines geeigneten Klassifikators erfordert. Daher ist die Wahl eines Klassifikators, der den Merkmalen des zu lösenden Analyseproblems entspricht, ein wichtiger Faktor für eine korrekte Lösung.
Die verschiedenen Arten von Klassifikatoren haben Vor- und Nachteile. Klassifikatoren, die statistische Methoden verwenden, haben beispielsweise eine gute mathematische Validität, sind aber schwierig zu verwenden und erfordern die Kenntnis der Wahrscheinlichkeitsverteilung der Rohdaten und die Schätzung ihrer Parameter (daher werden sie als parametrisch bezeichnet) sowie eine feste Modellstruktur. Darüber hinaus schätzen statistische Methoden nur die Wahrscheinlichkeit der Zugehörigkeit eines Objekts zu einer Klasse, aber sie "erklären" nicht warum.
Klassifikatoren, die auf maschinellem Lernen basieren, erfordern keine Schätzung der Parameter der Verteilung der Rohdaten, und ihr Ähnlichkeitsmaß wird durch eine Distanzfunktion (in der Regel euklidisch) formalisiert. Solche Klassifikatoren werden als metrische Klassifikatoren bezeichnet. Sie sind in der Regel einfacher zu implementieren und anzuwenden als parametrische Verfahren, und ihre Ergebnisse sind leichter zu interpretieren und zu verstehen. Gleichzeitig sind metrische Klassifikatoren aber auch heuristische Modelle - sie liefern nur in einer begrenzten Anzahl von praktisch bedeutsamen Fällen eine Lösung und können eine ungenaue oder nicht die einzige Lösung liefern. Deshalb müssen ihre Ergebnisse mit einer gewissen Vorsicht verwendet werden.
Ein gewisser Kompromiss zwischen parametrischen und metrischen Methoden ist die Verwendung von neuronalen Netzen zur Lösung von Klassifikationsproblemen. Bei den neuronalen Netzen handelt es sich nämlich um nichtparametrische Modelle, die keine Annahmen über die Wahrscheinlichkeitsverteilung der Daten erfordern, aber auch keine Abstandsmaße verwenden. Dies macht sie zu universellen Klassifikatoren, die auch in Fällen Ergebnisse liefern, in denen parametrische und metrische Klassifikatoren keine akzeptable Lösung bieten.
Merkmale der Verwendung neuronaler Netze als Klassifikatoren
Dabei ist zu beachten, dass das Klassifizierungsproblem bei neuronalen Netzen im Allgemeinen nicht das Hauptproblem ist (wie z. B. bei Entscheidungsbäumen oder k-nearest-neighbour-Algorithmen). Ursprünglich ist das Hauptziel von neuronalen Netzen die numerische Vorhersage (wobei die Eingabe und die Ausgabe des Modells numerische Werte sind, was manchmal fälschlicherweise als Regression bezeichnet wird).
Mit Hilfe spezieller Methoden der Datendarstellung ist es jedoch möglich, Neuronale Netze so anzupassen, dass sie mit kategorischen Daten umgehen können, d. h. kategorische Werte als Eingabe erhalten und kategorische Werte als Ausgabe erzeugen. Zu diesem Zweck werden kategorische Attribute mit numerischen Werten entsprechend kodiert.
Die Verwendung von neuronalen Netzen als Klassifikatoren hat jedoch eine Reihe von Vorteilen, die hervorgehoben werden können:
- Neuronale Netze sind selbstlernende Modelle, die wenig oder gar kein Eingreifen des Benutzers erfordern;
- Neuronale Netze sind universelle Approximatoren, mit denen sich jede kontinuierliche Funktion mit akzeptabler Genauigkeit approximieren lässt;
- Neuronale Netze sind nichtlineare Modelle, die eine effektive Lösung von Klassifizierungsproblemen auch bei fehlender linearer Trennbarkeit der Klassen ermöglichen (s. Abb. unten).

Es ist anzumerken, dass es keine spezifischen neuronalen Netzarchitekturen für die Klassifizierung gibt. Die am häufigsten verwendete Netzarchitektur für die Klassifizierung ist das Forward-Propagation-Netz, das die Merkmalswerte des zu klassifizierenden Objekts einliest und ein Label oder einen numerischen Klassencode ausgibt. In der Regel werden mehrschichtige Perseptrons verwendet. In solchen Netzen kommen die Elemente eines Merkmalsvektors an den Eingangsneuronen an und werden auf alle Neuronen der ersten versteckten Schicht des neuronalen Netzes verteilt, wodurch sich die Dimensionalität des Problems ändert.
Nachfolgende Schichten teilen also Objekte in Klassen im Merkmalsraum mit einer höheren Dimensionalität als der ursprüngliche Raum ein. Wenn beispielsweise die Dimensionalität des Merkmalsvektors der Originaldaten vier beträgt und die verborgene Schicht sechs Neuronen enthält, dann teilt die Ausgabeschicht die Merkmale in Klassen im sechsdimensionalen Raum ein.
Dies erhöht die Effizienz des Prozesses: Die richtige Wahl der Konfiguration und der Parameter des neuronalen Netzes ermöglicht es, gute Klassifizierungsergebnisse zu erzielen, selbst wenn die Klassifizierer anderer Typen, die nur in der Dimensionalität der Trainingsdaten arbeiten, keine akzeptablen Ergebnisse liefern. Der Nachteil ist, dass die Netzkonfiguration, die die Klassentrennungsfunktion im Merkmalsraum am besten approximiert, nicht im Voraus bekannt ist. Daher muss sie experimentell ausgewählt werden oder es muss auf Erfahrungen mit ähnlichen Lösungen zurückgegriffen werden.
Wenn die Verteilung der Klassen so ist, dass eine komplexe Funktion für ihre Aufteilung erforderlich ist, kann die Dimensionalität neuronaler Netze unannehmbar groß sein. In diesem Fall kann das Problem durch eine spezielle Vorverarbeitung der Eingabedaten gelöst werden.
Vorbereitung der Ausgangsdaten
Unabhängig davon, wie fortschrittlich die für die Klassifizierung verwendeten Methoden und Algorithmen sind, werden sie keine korrekten Ergebnisse liefern, wenn sie auf unsaubere Daten angewendet werden. Daher besteht der erste Schritt beim Aufbau eines auf einem neuronalen Netz basierenden Klassifizierungsmodells in der Vorverarbeitung und Bereinigung der Daten.
Der erste Schritt in diese Richtung ist die Auswahl von Merkmalen, die für die Unterscheidung von Klassen nützlich sind. In der Tat können Objekte in einem Bereich durch eine große Anzahl von Merkmalen beschrieben werden. Aber nicht alle können zuverlässig zwischen Objekten verschiedener Klassen unterscheiden. Wenn zum Beispiel Objekte verschiedener Klassen ungefähr die gleiche Größe haben, macht es keinen Sinn, "dimensionale" Merkmale zu verwenden. Es ist auch nicht wünschenswert, Merkmale zu verwenden, deren Werte zufällig sind und keine Muster in der Verteilung der Objekte zwischen den Klassen widerspiegeln.
Darüber hinaus ist es wichtig, die Anzahl der verwendeten Merkmale zu bestimmen. Je mehr Merkmale zur Erstellung eines Klassifikators verwendet werden, desto mehr Informationen werden zur Unterscheidung der Klassen verwendet. Dies erhöht jedoch die Rechenkosten und die Anforderungen an die Größe des neuronalen Netzes (die Anzahl der Parameter, die im Lernprozess angepasst werden können - Gewichte der Neuronenverbindungen). Andererseits verschlechtert eine Verringerung der Anzahl der verwendeten Merkmale die Trennbarkeit der Klassen. So kann es zum Beispiel vorkommen, dass Objekte verschiedener Klassen die gleiche Bedeutung von Merkmalen haben und ein Widerspruch entsteht.
Für die Einteilung der Kreditnehmer in "schlecht" und "gut" können beispielsweise nur zwei Merkmale ausgewählt werden: "Einkommen" und "Alter". Es ist wahrscheinlich, dass zwei Kreditnehmer gleichen Alters und gleichen Einkommens in unterschiedliche Klassen fallen würden. Zur Unterscheidung der Kreditnehmer sollte ein weiteres Attribut, z. B. die Anzahl der unterhaltsberechtigten Personen, hinzugefügt werden. Die Auswahl der Merkmale für das Training eines Klassifikators auf der Grundlage eines neuronalen Netzes ist daher eine Kompromisslösung.
Eine weitere wichtige Methode zur Vorverarbeitung der Trainingsdaten ist die Normalisierung der Attributwerte auf einen Bereich von 0...1. Die Normalisierung ist notwendig, da die Klassifizierungsattribute unterschiedlicher physikalischer Natur sind und sich ihre Werte um mehrere Größenordnungen unterscheiden können (z. B. "Einkommen" und "Alter").
Darüber hinaus sollte vor der Erstellung eines auf einem neuronalen Netz basierenden Klassifikators ein Datenprofil erstellt werden, um die Datenqualität zu bewerten, und, falls erforderlich, sollten Datenbereinigungswerkzeuge verwendet werden: Lücken füllen, anomale Werte und Ausreißer unterdrücken, Duplikate und Inkonsistenzen ausschließen.
Kodierung der Ausgabewerte
Der grundlegende Unterschied zwischen dem Klassifizierungsproblem und dem numerischen Vorhersageproblem besteht darin, dass die Ausgangsvariable diskret ist (die Klassenbezeichnung oder ihr numerischer Code). Da es sich bei neuronalen Netzen um Modelle mit überwachtem Lernen handelt, muss die Klassenvariable für jedes Trainingsbeispiel angegeben werden.
Im einfachsten Fall, wenn die Klassifizierung binär ist, kann das Problem durch ein neuronales Netz mit einem einzigen Neuron der Ausgabeschicht gelöst werden, das zwei mögliche Zustände ausgibt (zum Beispiel 0 und 1). Wenn es mehrere Klassen gibt, muss das Problem ihrer Repräsentation in der Ausgabe des Netzes gelöst werden. In der Praxis wird in der Regel der Ausgabevektor verwendet, dessen Elemente Labels oder Klassennummern sind.
In diesem Fall wird die Zugehörigkeit eines Objekts zu einer Klasse dadurch bestimmt, dass das entsprechende Element des Ausgangsvektors (das i-te Element für die j-te Klasse) auf 1 gesetzt wird, während die anderen Elemente auf 0 gesetzt werden. Dann entspricht beispielsweise die zweite Klasse am zweiten Ausgang des Netzes einer 1 und an den anderen 0.
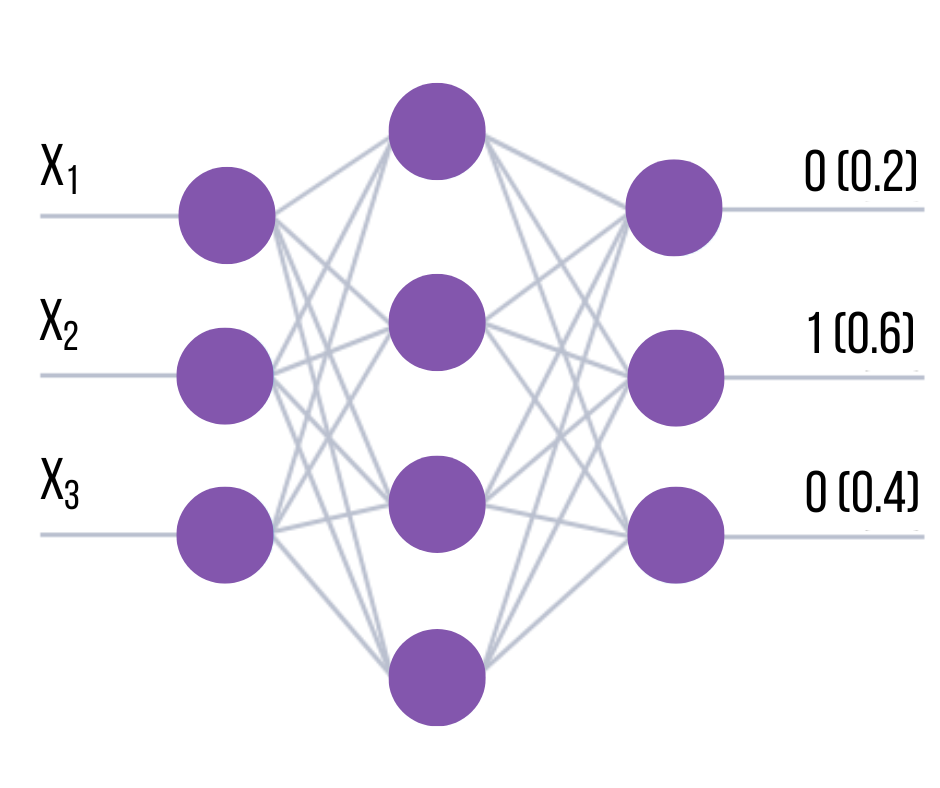
Für die Codierung können auch andere Werte außer 1 verwendet werden. Bei der Interpretation des Ergebnisses wird jedoch in der Regel davon ausgegangen, dass die Klasse durch die Nummer des Netzausgangs bestimmt wird, an dem der Höchstwert auftrat. Wenn beispielsweise ein Vektor von Ausgangswerten (0,2 0,6 0,4) am Ausgang des Netzes erzeugt wurde, hat die zweite Komponente des Vektors den höchsten Wert. Folglich wäre die Klasse, auf die sich dieses Beispiel bezieht, 2.
Bei dieser Art der Kodierung gilt: Je mehr sich der Maximalwert von den anderen unterscheidet, desto sicherer ist es, dass das Netz das Objekt der Klasse zugeordnet hat. Formal kann dieses Vertrauen als Index eingegeben werden, der gleich der Differenz zwischen dem Höchstwert am Eingang des Netzes (der die Klassenzugehörigkeit bestimmt) und dem nächstliegenden Wert am anderen Ausgang ist.
Für das obige Beispiel wird die Konfidenz des Netzes, dass das Beispiel zur zweiten Klasse gehört, als Differenz zwischen der zweiten und dritten Komponente des Vektors bestimmt und ist gleich 0,6-0,4=0,2. Je höher die Konfidenz, desto höher die Wahrscheinlichkeit, dass das Netz die richtige Antwort gegeben hat. Diese Kodierungsmethode ist die einfachste, aber nicht immer die effizienteste Art der Darstellung von Klassen in der Ausgabe des Netzes.
Bei einer anderen Darstellungsmethode wird beispielsweise die Klassennummer in binärer Form im Ausgangsvektor des Netzes kodiert. Wenn die Anzahl der Klassen 5 beträgt, reichen drei Ausgangsneuronen aus, um sie zu repräsentieren, und der Code, der z. B. der dritten Klasse entspricht, ist 011. Der Nachteil dieses Ansatzes ist die fehlende Möglichkeit, den Konfidenzindex zu verwenden, da die Differenz zwischen beliebigen Elementen des Ausgangsvektors immer gleich 0 oder 1 ist. Folglich führt die Änderung eines beliebigen Elements des Ausgangsvektors unweigerlich zu einem Fehler. Daher ist es sinnvoll, den Hamming-Code zu verwenden, um den "Abstand" zwischen den Klassen zu vergrößern, was die Klassifizierungsgenauigkeit erhöht.
Ein anderer Ansatz besteht darin, das Problem mit k Klassen in k∗(k-1)/2 Teilaufgaben mit je zwei Klassen aufzuteilen (2-by-2-Kodierung). Die Teilaufgabe besteht in diesem Fall darin, dass das Netz das Vorhandensein einer Komponente des Vektors feststellt. D.h. der Ausgangsvektor wird in Gruppen von je zwei Komponenten aufgeteilt, so dass alle möglichen Kombinationen der Komponenten des Ausgangsvektors in diese Gruppen aufgenommen werden. Aus der Kombinatorik ist bekannt, dass die Anzahl dieser Gruppen als die Anzahl der ungeordneten Stichproben ohne Wiederholungen von zwei der ursprünglichen Komponenten definiert werden kann:
Für eine Aufgabe mit vier Klassen gibt es dann beispielsweise sechs Ausgaben (Teilaufgaben), die wie folgt verteilt sind:
| Teilaufgabe (Output) | Klassen |
|---|---|
| 1 | 1-2 |
| 2 | 1-3 |
| 3 | 1-4 |
| 4 | 2-3 |
| 5 | 2-4 |
| 6 | 3-4 |
Hier zeigt eine 1 in der Ausgabe das Vorhandensein einer der Komponenten an. Bestimmen Sie dann die Klassennummer aus dem Ergebnis der Netzberechnung wie folgt: Ermitteln Sie, welche Kombinationen einen einzigen (oder annähernd einen) Ausgabewert erhalten haben (d. h. welche Teilaufgaben aktiviert wurden), und nehmen Sie an, dass die Klassennummer diejenige sein sollte, die in der größten Anzahl aktivierter Teilaufgaben enthalten war (siehe Tabelle).
| Klasse | Teilaufgaben (Outputs) |
|---|---|
| 1 | 1, 2, 3 |
| 2 | 1, 4, 5 |
| 3 | 2, 4, 6 |
| 4 | 3, 5, 6 |
Diese Kodierungsmethode liefert bei vielen Aufgaben bessere Klassifizierungsergebnisse als klassische Ansätze.
Auswahl der Größe des Netzes
Um einen effizient funktionierenden Klassifikator zu erstellen, ist es sehr wichtig, die richtige Größe des Netzes zu wählen, d. h. die Anzahl der Verbindungen zwischen den Neuronen, die im Lernprozess eingerichtet werden und die Eingabedaten verarbeiten, wenn der Prozess läuft. Wenn die Anzahl der Gewichte im Netz klein ist, kann es keine komplexen Klassentrennungsfunktionen implementieren. Andererseits führt eine Erhöhung der Anzahl der Verbindungen zu einer Steigerung der Informationskapazität des Modells (Gewichte wirken als Speicherelemente).
Wenn die Anzahl der Verknüpfungen im Netz die Anzahl der Trainingsbeispiele übersteigt, wird das Netz die Abhängigkeiten in den Daten nicht annähern, sondern sich einfach an die Eingabe-Ausgabe-Kombinationen aus den Trainingsbeispielen erinnern und diese reproduzieren. Dieser Klassifikator wird mit den Trainingsdaten gut funktionieren und bei den neuen Daten, die nicht in den Trainingsprozess einbezogen waren, willkürliche Antworten produzieren. Mit anderen Worten: Das Netz wird keine Generalisierungsfähigkeit erlangen, und der auf seiner Grundlage erstellte Klassifikator wird in der Praxis nutzlos sein.
Es gibt zwei Ansätze, einen konstruktiven und einen destruktiven, um das Netz richtig zu dimensionieren. Die erste besteht darin, zunächst ein Netz mit minimaler Größe zu nehmen, das dann schrittweise vergrößert wird, bis die erforderliche Genauigkeit erreicht ist. Nach jeder Erhöhung wird sie neu trainiert. Es gibt auch die sogenannte Kaskaden-Korrelationsmethode, bei der die Netzarchitektur nach jeder Trainingsepoche angepasst wird, um den Fehler zu minimieren.
Beim destruktiven Ansatz nehmen wir zunächst ein überdimensioniertes Netz und entfernen dann die Neuronen und Verbindungen, die sich am wenigsten auf die Genauigkeit des Klassifikators auswirken. Es ist nützlich, sich an die folgende Regel zu erinnern: Die Anzahl der Beispiele in der Trainingsmenge muss größer sein als die Anzahl der abstimmbaren Gewichte des Netzes. Andernfalls ist das Netz nicht in der Lage, sich zu verallgemeinern, und erzeugt willkürliche Werte für die neuen Daten.
Um die Generalisierungsfähigkeit des Netzes, auf dessen Grundlage der Klassifikator erstellt wird, zu überprüfen, ist es sinnvoll, einen Testsatz zu verwenden, der aus zufällig ausgewählten Beispielen des Trainingsdatensatzes gebildet wird. Die Beispiele des Testsatzes nehmen nicht am Trainingsprozess des Netzes teil (d. h. sie haben keinen Einfluss auf die Anpassung seiner Gewichte), sondern werden einfach zusammen mit den Trainingsbeispielen in den Eingang des Netzes eingespeist.
Wenn das Netz sowohl auf der Trainingsmenge als auch auf der Testmenge (deren Beispiele die Rolle der neuen Daten spielen) eine hohe Genauigkeit aufweist, kann man sagen, dass das Netz die Fähigkeit zur Generalisierung erreicht hat. Wenn ein Netz nur bei den Trainingsdaten gute und bei den Testdaten schlechte Ergebnisse erzielt, ist es nicht generalisierungsfähig.
Der Netzfehler wird oft als Trainingsfehler in der Trainingsmenge und als Generalisierungsfehler in der Testmenge bezeichnet. Das Verhältnis von Trainings- und Testsätzen kann beliebig groß sein. Der Testsatz muss genügend Beispiele enthalten, damit das Modell richtig trainiert werden kann.
Die offensichtliche Möglichkeit, die Generalisierungsfähigkeit des Netzes zu verbessern, besteht darin, die Anzahl der Trainingsbeispiele zu erhöhen oder die Anzahl der Verbindungen zu verringern. Ersteres ist aufgrund der begrenzten Datenmenge und des erhöhten Rechenaufwands nicht immer möglich. Eine Verringerung der Anzahl der Verbindungen beeinträchtigt dagegen die Genauigkeit des Netzes. Daher ist die Wahl der Modellgröße oft recht komplex und erfordert wiederholte Versuche.
Auswahl der Netzarchitektur
Wie bereits erwähnt, werden für die Lösung des Klassifizierungsproblems keine speziellen neuronalen Netzarchitekturen verwendet. Die typische Lösung hierfür sind flache Netze mit sequentiellen Verbindungen (Perseptrons). In der Regel werden mehrere Netzkonfigurationen mit unterschiedlicher Anzahl von Neuronen und deren Organisation in Schichten getestet.
In diesem Fall ist der Hauptindikator für eine Wahl der Umfang der Trainingsmenge und die Erreichung der Generalisierungsfähigkeit des Netzes. In der Regel wird ein Backpropagation-Lernalgorithmus mit einer Validierungsmenge verwendet.
Algorithmus zur Erstellung eines Klassifikators
Der Aufbau eines auf einem neuronalen Netz basierenden Klassifikators umfasst eine Reihe von Schritten.
- Vorbereitung der Daten
- Erstellung einer Datenbank mit Beispielen, die für die Aufgabe typisch sind
- Aufteilung des gesamten Datensatzes in zwei Sätze: Training und Test (eine Aufteilung in 3 Sätze ist möglich: Training, Test und Validierung)
- Vorverarbeitung der Daten
- Auswahl der Merkmale, die für die Klassifizierungsaufgabe relevant sind.
- Transformation und ggf. Bereinigung der Daten (Normalisierung, Beseitigung von Duplikaten und Inkonsistenzen, Entfernung von Ausreißern usw.). Infolgedessen ist es wünschenswert, einen linear nach Klassen getrennten Raum von Beispielsätzen zu erhalten.
- Auswahl des Ausgangskodierungssystems
- Konzeption, Training und Qualitätsbewertung des Netzes
- Auswahl der Netztopologie: Anzahl der Schichten, Anzahl der Neuronen in den Schichten, usw.
- Auswahl der Aktivierungsfunktion der Neuronen (z. B. logistisch, hypertangential, usw.)
- Auswahl des Lernalgorithmus
- Abschätzung der Netzleistung auf der Grundlage der Validierungsmenge oder anderer Kriterien, um die Architektur zu optimieren (Verringerung der Gewichte, Ausdünnung des Merkmalsraums)
- Entscheidung für die Version des Netzes, die die beste Verallgemeinerungsfähigkeit bietet, und Bewertung der Qualität der Leistung auf dem Testsatz
- Verwendung und Diagnose
- Herausfinden, inwieweit verschiedene Faktoren die Entscheidung beeinflussen (heuristischer Ansatz)
- Überprüfung, ob das Netz die erforderliche Klassifizierungsgenauigkeit erreicht (die Anzahl der falsch erkannten Beispiele ist gering)
- Gehen Sie gegebenenfalls zu Schritt 2 zurück und ändern Sie die Art und Weise, wie die Beispiele präsentiert werden, oder ändern Sie die Datenbank
- Praktische Nutzung des Netzes zur Lösung des Problems
Um einen effektiven Klassifikator zu erstellen, müssen die Eingabedaten von guter Qualität sein. Keine auf neuronalen Netzen oder statistischen Methoden basierende Klassifizierungsmethode wird jemals die gewünschte Modellqualität liefern, wenn die verfügbare Menge an Beispielen nicht ausreichend vollständig und repräsentativ für das zu lösende Problem ist.